complexity measures in algos
Complexity Measures:
Complexity - approx measure of algo efficiency
2 kinds:
- Time Complexity
- Space Complexity
Factors impacting algo efficiency:
- single or multi processor machine
- read/write speed to RAM
- 32 bit / 64 bit architecture
- disk usage
- input
All factors except input will vary based on the machine the algo is running on, so we can’t control it. We measure the rate of growth of time or memory space with respect to the growth in input - this measure that is called the time or space complexity of an algorithm.
Interviewer may ask you either:
- algo of your code or
- to improve complexity of a given algorithm.
Time complexity
Growth of time taken for an algorithm to run, wrt growth in input size.
Assumptions to calculate time complexity of an algo:
- single processor machine
- 32 bit architecture
- sequential code run - no parallel processing
- take constant time for basic operations
Basic Operations are:
- variable assignment:
int x = 1; - variable comparison:
if (x == 1) {} - arithmetic operation:
x + 1 - unit operation:
System.out.println("1 unit operation");
This means x = x + 1 takes 1 + 1 = 2 units of time as it has a variable assignment and an arithmetic operation.
Time Complexity is calculated by considering the size of the input and the problem itself, meaning:
- list the basic operations
- count the number of times each is executed
- sum all counts to get an equation
- ignore the lower order terms and constant coefficients
For Example:
public class main {
public static int addOne(int x) {
x += 1;
return x;
}
int temp = addOne(5);
}This code has 3 basic operations:
- 1 arithmetic operation -
x + 1 - 1 variable assignment -
x = (x + 1) - 1 basic operation -
return x
As per above - total time complexity of above code is 3 units of time
Examples:
Example 1: Measuring Time Complexity - Simple Loop of Size N
The following code runs a simple loop to count the number of iterations:
class Sum {
public static void main(String args[]) {
int n = 10; // 1 step
int sum = 0; // 1 step
for (int i = 0; i < n; i++) {
sum += 1; // n steps
}
System.out.println(sum); // 1 step
}
}The code above has:
- 2 direct variable assignments:
int n = 10;,int sum = 0; - 1 unit operation:
System.out.println(sum); - 1 for loop:
for (int i = 0; i < n; i++)
A for loop consists of the following:
- initialization
- comparison
- incrementation
- operations running inside the loop.
Now let’s break down the for loop further, it has:
- For loop definition -
for (int i = 0; i < n; i++):- 1 variable assignment:
int i = 0;= initialization - 1 variable comparison:
i < n=>if (i < n)= comparison - 1 variable assignment + 1 arithmetic operation:
i++=>i = i + 1= incrementation
- 1 variable assignment:
- Inside the loop:
- 1 variable assignment + 1 arithmetic operation:
sum += 1;=>sum = sum + 1
- 1 variable assignment + 1 arithmetic operation:
So if we now count the number of operations, we have:
- 1 unit of time for
int n = 10; - 1 unit of time for
int sum = 0; - 1 unit of time for
int i = 0;= loop initialization - n + 1 unit of time for
i < n=>if (i < n)= loop comparison happens n times for n inputs, + 1 time for breaking the loop - 2n units of time for
sum += 1;=>sum = sum + 1= 2 units for each iteration upto n times - 2n unit of time for
i++=>i = i + 1= loop incrementation happens n times for n inputs - 1 unit of time for
System.out.println(sum);
Forming the equation:
1 + 1 + 1 + (n + 1) + 2n + 2n + 1 = 5 + 5n
Example 2: Measuring Time Complexity - Nested Loop
The following code runs a nested loop:
class NestedLoop {
public static void main(String[] args) {
int n = 5; // 1 step
int sum = 0; // 1 step
for (int i = 0; i < n; i++) { // n steps
for (int j = 0; j < n; j++) { // n * n steps
sum++; // n * n steps
}
}
System.out.println("Sum: " + sum); // 1 step
}
}Counting the number of operations, we have:
- 1 unit of time for
int n = 5; - 1 unit of time for
int sum = 0; - 1 unit of time for
int i = 0;= loop initialization - n + 1 unit of time for
i < n=>if (i < n)= loop comparison happens n times for n inputs, + 1 time for breaking the loop- n x 1 unit of time for
int j = 0;= inner loop initialization happens n times for n iterations - n x (n + 1) unit of time for
j < n=>if (j < n)= inner loop comparison happens n times for n inputs, + 1 time for breaking the inner loop - n x 2n units of time for
sum ++;=>sum = sum + 1= 2 units for each iteration upto n times in the inner loop - n x 2n units of time for
j++=>j = j + 1= inner loop incrementation happens n times for n inputs
- n x 1 unit of time for
- 2n unit of time for
i++=>i = i + 1= loop incrementation happens n times for n inputs - 1 unit of time for
System.out.println("Sum: " + sum);
Forming the equation:
1 + 1 + 1 + (n + 1) + (n x 1 + n x (n + 1) + n x 2n + n x 2n) + 2n + 1 = 5n^2 + 5n + 5
Asymptotic Analysis and the Big O:
Mathematically, asymptotic behavior of a function f(n) refers to the growth of f(n) as n gets large.
Algos can be put into broad categories, based on their run time complexity. Asymptotic Analysis defines time complexity of the algorithm as a f(n), where n in the size of the input.
Big O - O(n)
The Big O complexity refers to the efficiency of an algorithm in the worst case scenario, which means that the performance of the algorithm cannot be worse than it’s Big O complexity for large input sizes.
To compute Big O complexity of an algorithm from the running time complexity equation, drop the leading constants and ignore the lower order terms.
For example, Big O complexity of an algorithm with time complexity = 3n^3 + 4n + 2 is in O(n^3).
Big O complexity gives an upper bound on the running time complexity of an algorithm.
List of Big O complexities in the order of most efficient to least efficient
| Function | Name | Function | Name |
|---|---|---|---|
| 1. O(1) | Constant | 7. (O(n^2) | Quadratic |
| 2. O(log n) | Logarithmic | 8. (O(n^3) | Cubic |
| 3. O(log^2 n) | Log-Square | 9. (O(n^4) | Quartic |
| 4. O(sqrt(n)) | Root-N | 10. (O(2^n) | Exponential |
| 5. O(n) | Linear | 11. (O(e^n) | Exponential |
| 6. O(n log n) | Linearithmic | 12. (O(n!) | n-Factorial |
Time Complexity Graph:
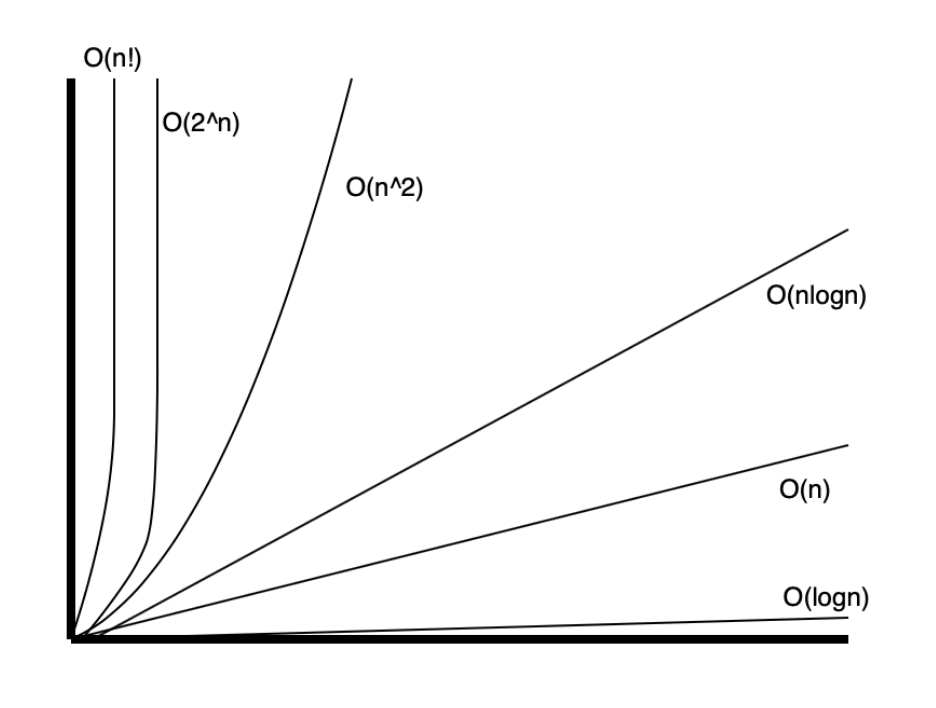
As an example, if we consider e^3n, its complexity is NOT in O(e^n).
Reason? –> e^3n = e^(2n+n) = e^2n x e^n. So for n > 0, e^3n > e^n, which is why e^3n is NOT in O(e^n)
Why Big O trumps them all:
Big Omega - Omega(n)
The Big Omega complexity of an algorithm refers to the efficiency of the algorithm with respect to the growth of input size in the BEST CASE SCENARIO. This means the efficiency of the algorithm cannot be better than the Big Omega complexity for large input sizes.
For example, if the time complexity of an algorithm is f(n) = n^2, it cannot be better then Omega(n) and cannot be better than Omega(n^2), but it is better than Omega(n^3) => f(n) is in Omega(n) and Omega(n^2), but not in Omega(n^3).
So formally, if there exists a constant c > 0 an there exists an n_0 > 1 and f(n) >= c x g(n) for n > n_0, then f(n) is in Omega(g(n)).
Big Theta - Theta(n)
The Big Theta complexity of an algorithm refers to the efficiency of the algorithm with respect to the growth of input size in the Average Case Scenario. This means that there exits 2 constants, c1 and c2, so that efficiency of the algorithm is in between c1.Theta(n) and c2.Theta(n).
For example, if the time complexity of an algorithm is f(n) = n^2, it is between 2 x n^2 and 0.5 x n^2, so f(n) = n^2 is in Theta(n^2). but n^2 is not in Theta(n^3) and not in Theta(n).
Little O - o(n)
Time Complexity of an algorithm, f(n) is in o(g(n)) if f(n) is strictly less than c x g(n), where c > 0.
For example n + 10 is in o(n^2) as n+10 < n^2 for all c > 0. Similarly n+10 is in o(10^n), is in o(nlog(n)), but not in o(n) and not in o(n-10)
Little omega - little_omega(n)
Time Complexity of an algorithm, f(n) is in little_omega(g(n)) if f(n) is strictly greater than c x g(n), where c > 0.
For example 5 x n^2 is in little_omega(n), as 5 x n^2 > n for all c > 0. Similarly, 5 x n^2 is in little_omega(1), but not in little_omega(n^2).
Essentially we learnt that:
- If our algorithm is in o(n) then it’s performance is < n
- If our algorithm is in O(n) then it’s performance is <= n
- If our algorithm is in Theta(n) then it’s performance is = n
- If our algorithm is in Omega(n) then it’s performance is >= n
- If our algorithm is in little_omega(n) then it’s performance is > n
This leads us to the understanding that o(n) signifies the absolute worst case scenario when it comes to the efficiency of the algorithm in question, however Big O(n) also considers the case when the algorithm performance is equal to growth in put size n.
To clarify this further, consider a robot, which is assigned to look for a red ball in a series of 5 boxes with 100 balls each. All balls are yellow except this ball. We assume that the robot uses a simple algorithm of search for the ball in each box by investigating every single ball.
The best case scenario is that the first ball the robot picks from the first box is the red ball. And the worst case scenario is that the robot has to look through all the balls in all the boxes and the last ball it considers turns out to be the last one.
We get a good measure of the robot’s algorithm by considering the worst case scenario as the efficiency of the algorithm cannot be better than that. This means that the robot will be able to find the red ball for sure in the time taken to process the worst case scenario. This is why we consider the Big O(n).
Useful Formulae
- Sum(c)(i = 1 to n) = c + c + c + c + … + c = c x n
- Sum(i)(i = 1 to n) = 1 + 2 + 3 + 4 + … + n = 1/2 x n(n+1)
- Sum(i^2)(i = 1 to n) = 1 + 4 + 9 + 16 + … + n^2 = 1/6 x n(n+1)(2n+1)
- Sum(r^i)(i = 0 to n) = r^0 + r^1 + r^2 + r^3 + … + r^n = 1/(r-1) x (r^(n+1) - 1)
General Tips
- Every time a list get iterated over c x length times, most likely is runs in O(n)
- When the number of elements in problem space are reduced by half or another factor, run time complexity is O(log n)
- In case of a single nested loop, most likely run time complexity is in O(n^2)
Common Complexity Scenarios
Simple For Loop
for (int x = 0; x < n; x++) {
// statement(s) that take constant time
}Analyzing the above code, it contains:
- 1 assignment operation
int x = 0 - n + 1 variable comparisons
x < n=>if (x < n) - n x c unit operations (assuming there are c statements running for n iterations each time)
- n x (1 arithmetic operation + 1 variable assignment)
x++=>x = x + 1running for n iterations n times
So the run time complexity of the above code is 1 + (n + 1) + cn + 2n = (3n + 2) + cn
To compute Big O, we drop the leading constants and ignore the lower order terms.
Considering T(n) = (3n + 2) + cn, this means Run Time Complexity = n + n = 2n => O(n)
For-loop with increments
for (int x = 0; x < n; x = x + k) {
// statement(s) that take constant time
}Analyzing the above code, it contains:
- 1 assignment operation
int x = 0 - n/k + 1 variable comparisons
x < n=>if (x < n) - n/k x c unit operations (assuming there are c statements running for n iterations each time)
- n/k x (1 arithmetic operation + 1 variable assignment)
x = x + kincrementing by k each iteration for n iterations
So the run time complexity of the above code is 1 + (n/k + 1) + cn/k + 2n/k = (3n/k + 2) + cn/k
To compute Big O, we drop the leading constants and ignore the lower order terms.
Considering T(n) = (3n/k + 2) + cn/k, this means Run Time Complexity = n + n = 2n => O(n)
Simple nested For-loop
for (int i = 0; i < n; i++) {
for (int x = 0; x < m; x++) {
// Statement(s) that take(s) constant time
}
}Analyzing the above code, it contains:
- 1 assignment operation
int i = 0 - n + 1 variable comparisons
i < n=>if (i < n)- n x 1 assignment operations
int x = 0; - n x m + 1 variable comparisons
x < m=>if (x < m) - n x m x c unit operations (assuming there are c statements running for n iterations each time)
- n x m x (1 arithmetic operation + 1 variable assignment)
x++=>x = x + 1
- n x 1 assignment operations
- n x (1 arithmetic operation + 1 variable assignment)
i++=>i = i + 1
So the run time complexity of the above code is 1 + (n + 1) + n + nm + 1 + nmc + 2nm + 2n = (3nm + 4n + 3) + nmc
To compute Big O, we drop the leading constants and ignore the lower order terms.
Considering T(n) = (3nm + 4n + 3) + nmc , this means Run Time Complexity = nm + nm = 2nm => O(n x m)
Nested For-loop with dependent variables
for (int i = 0; i < n; i++ ) {
for (int x = 0; x < i; x++) {
// Statement(s) that take(s) constant time
}
}Analyzing the above code, the inner loop runs i times for every i’th iteration of outer loop. This implies the inner loop runs 1 time, then 2 times, then 3 times and so on until n times.
So counting the times inner loop runs we have arithmetic series: 0 + 1 + 2 + 3 + .. + (n - 1) = 1/2 x (n - 1) x ((n - 1) + 1)
Considering the above statements, we have the following:
- 1 assignment operation
int i = 0 - n + 1 variable comparisons
i < n=>if (i < n)- n x 1 assignment operations
int x = 0; - [1/2 x (n - 1) x ((n - 1) + 1)] + 1 variable comparisons
x < m=>if (x < m) - [1/2 x (n - 1) x ((n - 1) + 1)] x c unit operations (assuming there are c statements running for n iterations each time)
- [1/2 x (n - 1) x ((n - 1) + 1)] x (1 arithmetic operation + 1 variable assignment)
x++=>x = x + 1
- n x 1 assignment operations
- n x (1 arithmetic operation + 1 variable assignment)
i++=>i = i + 1
So the run time complexity of the above code is 1 + (n + 1) + n + [1/2 x (n - 1) x ((n - 1) + 1)] + 1 + [1/2 x (n - 1) x ((n - 1) + 1)] x c + 2 x [1/2 x (n - 1) x ((n - 1) + 1)] + 2n = (3+c)/2 x n(n-1) + 4n + 3 = (3+c)/2 x n^2 + (5-c)/2 x n + 3
To compute Big O, we drop the leading constants and ignore the lower order terms.
Considering T(n) = (3+c)/2 x n^2 + (5-c)/2 x n + 3 , this means Run Time Complexity = n^2 => O(n^2)
Nested For-loop with doubling index
for (int i = 1; i <= n; i *= 2) {
for (int j = 0; j < i; j++) {
// Statement(s) that take(s) constant time
}
}Analyzing the above code, outer loop runs the number of times the index doubles until it gets to n. Which means to get to say n = 128, the loop runs 8 times (i = 1, 2, 4, 8, 16, 32, 64, 128) and 1 more time for the loop break iteration. So total 9 times. Now the inner loop runs for 1 time (+1 for loop breaker) for the first outer loop iteration, then for 2 (+1) times, then 4 (+1), then 8 (+1), then 16 (+1), then 32 (+1), then 64 (+1) and finally 128 (+1) times in the final outer loop iteration.
Formally, for n = 128, total outer loop runs = 9 => log_2(128) + 2, total inner loop runs = 1(+1) + 2(+1) + 4(+1) + 8(+1) + 16(+1) + 32(+1) + 64(+1) + 128(+1) = 2^0(+1) + 2^1(+1) + 2^2(+1) + .. + 2^7(+1) = 255 + 8 = (2*128 - 1) + (9 - 1). This means for input of size n, outer loop runs log_2(n) + 2 times and inner loop runs 2n - 1 + (log_2(n) + 1) times.
Considering the above statements, we have the following:
- 1 assignment operation
int i = 0 - (log_2(n) + 2) variable comparisons
i <= n=>if (i < n)- (log_2(n) + 2) x 1 assignment operations
int j = 0; - (log_2(n) + 2) x (2n - 1 + (log_2(n) + 1) x 1) variable comparisons
j < i=>if (j < i) - (log_2(n) + 2) x (2n - 1 + (log_2(n) + 1) x c) unit operations (assuming there are c statements running for n iterations each time)
- (log_2(n) + 2) x (2n - 1 + (log_2(n) + 1) x (1 arithmetic operation + 1 variable assignment))
j++=>j = j + 1
- (log_2(n) + 2) x 1 assignment operations
- (log_2(n) + 2) x (1 arithmetic operation + 1 variable assignment)
i *= 2=>i = i * 2
So the run time complexity of the above code is O(n) = 1 + (log_2(n) + 2) + (log_2(n) + 2) x 1 + (log_2(n) + 2) x (2n - 1 + (log_2(n) + 1) x 1) + (log_2(n) + 2) x (2n - 1 + (log_2(n) + 1) x c) + (log_2(n) + 2) x (2n - 1 + (log_2(n) + 1) x 2 + (log_2(n) + 2) x 2
Ignoring constants and higher order terms:
O(n) = 1 + log_2(n) + log_2(n) + log_2(n) x (2n + log_2(n)) + log_2(n) x (2n + log_2(n)) x c + log_2(n) x (2n + log_2(n)) x 2 + log_2(n) x 2
= 2log_2(n) + 2nlog_2(n) + log_2(n)log_2(n) + 2nlog_2(n)c + log_2(n)log_2(n)c + 4nlog_2(n) + 2log_2(n)log_2(n) + 2log_2(n)
= 4log_2(n) + (6+2c)nlog_2(n) + (3+c)(log_2(n)log_2(n))
= log_2(n) + nlog_2(n) + log_2(n)log_2(n)
= nlog_2(n)
This means Run Time Complexity = n x log_2(n) => O(nlog_2(n))
For-loop with log(n) complexity
int i = // any positive constant
int n = // any positive constant
int k = // any constant greater than 1
while (i < n) {
i *= k
// Statement(s) that take(s) constant time
}Like previous section, we see that the looping index multiplies with k every time the loop iterates. This cuts the number of iterations by k times, meaning the number of iterations is log_k(n).
Say i = 1, n = 27, k = 3, means to get to n = 27, the loops runs 4 times and 1 more time to break the loop. So total of 5 times. Meaning log_3(27) + 2 times. Say i = 1, n = 16, k = 2, means to get to n = 16, the loops runs 5 times and 1 more time to break the loop. So total of 6 times. Meaning log_2(16) + 2 times.
In general, for a loop with multiplying index k, time complexity is log_k(n).
This means Run Time Complexity = log_k(n) => O(log_k(n))
Challenges
Challenge 1 - Big O of Nested Loop with Addition
Problem Code
class NestedLoop {
public static void main(String[] args) {
int n = 10;
int sum = 0;
double pie = 3.14;
for (int var = 1; var < n; var = var + 3) {
System.out.println("Pie: " + pie);
for (int j = 1; j < n; j = j + 2) {
sum++;
}
System.out.println("Sum = " + sum);
} //end of outer for loop
} //end of main
} //end of classEquation
T(n) = 1 + 1 + 1 + 1 + (n/3 + 1) + n/3 + n/3 x (1 + (n/2 + 1) + 2 x n/2 + 2 x n/2) + n/3 + 2 x n/3
= 1 + 1 + 1 + 1 + n/3 + 1 + n/3 + n/3 + n/3 x n/2 + n/3 + 2n/3 x n/2 + 2n/3 x n/2 + n/3 + 2n/3
= 5 + 7n/3 + 5n/3 x n/2
= 1/6 x (30 + 14n + 5n^2)
= O(n^2)
Challenge 2 - Big O of Nested Loop with Subtraction
Problem Code
class NestedLoop {
public static void main(String[] args) {
int n = 10; // O(time complexity of the called function)
int sum = 0; //O(1)
double pie = 3.14; //O(1)
//O(?)
for (int var = n; var >= 1; var = var - 3) {
System.out.println("Pie: " + pie);
//O(?)
for (int j = n; j >= 0; j = j - 1) {
sum++;
}
System.out.println("Sum: " + sum);//O(1)
} //end of outer for loop
} //end of main
} //end of classEquation
T(n) = 1 + 1 + 1 + 1 + (n/3 + 2) + (n/3 + 1) + (n/3 + 1) x (1 + (n + 2) + 2 x (n + 1) + 2 x (n + 1)) + (n/3 + 1) + 2 x (n/3 + 1)
= 1 + 1 + 1 + 1 + n/3 + 2 + n/3 + 1 + n/3 + n/3 x n + 2n/3 + 2n x n/3 + 2n/3 + 2n x n/3 + 2n/3 + 1 + n + 2 + 2n + 2 + 2n + 2 + n/3 + 1 + 2n/3 + 2
= 17 + 27n/3 + 5n^2/3
= O(n^2)
Challenge 3 - Big O of Nested Loop with Multiplication
Problem Code
class NestedLoop {
public static void main(String[] args) {
int n = 10; // O(time complexity of the called function)
int sum = 0; //O(1)
double pie = 3.14; //O(1)
int var = 1;
//O(?)
while(var < n) {
System.out.println("Pie: " + pie);
//O(?)
for (int j = 0; j < var; j++) {
sum++;
}
var *= 2;
} //end of while loop
System.out.println("Sum: " + sum); //O(1)
} //end of main
} //end of classEquation
T(n) = 1 + 1 + 1 + 1 + (log_2(n) + 1) + log_2(n) + log_2(n)(1 + (2n - 1) + 1 + 2(2n - 1) + 2(2n - 1)) + 2log_2(n) + 1
= 6 + 2 log_2(n) + log_2(n) + 2n log_2(n) + 4n log_2(n) + 4n log_2(n) - 4 log_2(n) + 2 log_2(n)
= 6 + log_2(n) + 10n log_2(n)
= O(n log_2(n))
Challenge 4 - Nested Loop with Multiplication (Advanced)
Problem Code
class NestedLoop {
public static void main(String[] args) {
int n = 10; // O(time complexity of the called function)
int sum = 0; //O(1)
double pie = 3.14; //O(1)
int var = 1;
//O(?)
while(var < n) {
System.out.println("Pie: " + pie);
//O(?)
for (int j = 1; j < n; j = j + 2) {
sum++;
}
var *= 3;
} //end of while loop
System.out.println("Sum: " + sum); //O(1)
} //end of main
} //end of classEquation
T(n) = 1 + 1 + 1 + 1 + log_3(n) + 1 + log_3(n) + log_3(n) x (1 + n/2 + 1 + 2n/2 + 2n/2) + 2log_3(n) + 1
= 6 + 2log_3(n) + 2log_3(n) + n/2 x log_3(n) + 2n x log_3(n) + 2log_3(n)
= 6 + 6log_3(n) + 5n/2 x log_3(n)
= O(n log_3(n))
Challenge 5 - Nested Loop with Multiplication (Complex)
Problem Code
class NestedLoop {
public static void main(String[] args) {
int n = 10; //O(1)
int sum = 0; //O(1)
int j = 1; //O(1)
double pie = 3.14; //O(1)
//O(?)
for (int var = 1; var < n; var += 3) {
System.out.println("Pie: " + pie);
j = 1;
while (j < n) { //O(?)
sum += 1;
j *= 3;
} //end of while loop
} //end of for loop
System.out.println("Sum: " + sum); //O(1)
} //end of main
} //end of classEquation
T(n) = 1 + 1 + 1 + 1 + 1 + n/3 + 1 + n/3 + n/3 + n/3 ( log_3(n) + 1 + 2 log_3(n) + 2 log_3(n)) + 2n/3 + 1
= 6 + 3n/3 + 5n/3 log_3(n) + n/3 + 2n/3 + 1
= 7 + n + 5n/3 log_3(n) + 3n/3
= 7 + 2n + 5n/3 log_3(n)
= O(n log_3(n))
Challenge 6 : Nested Loop with Multiplication (Pro)
Problem Code
class NestedLoop {
public static void main(String[] args) {
int n = 10;
int sum = 0;
double pie = 3.14;
for (int var = 0; var < n; var++) {
int j = 1;
System.out.println("Pie: " + pie);
while(j < var) {
sum += 1;
j *= 2;
}
} //end of for loop
System.out.println("Sum: " + sum);
} //end of main
} //end of classEquation
Analyzing the code above, the inner loop runs for log_2(var) number of times, and var increments by 1 every iteration.
Number of inner loop runs = log_2(1) + log_2(2) + .. + log_2(n)
= log_2(1 x 2 x .. x n-1 x n)
= log_2(n!)
So then we have the following:
T(n) = 1 + 1 + 1 + 1 + n + 1 + n + n + log_2(n!) + 1 + 2log_2(n!) + 2log_2(n!) + 2n + 1
= 5 + 3n + 5nlog_2(n!) + 1 + 2n + 1
= 7 + 5n + 5 log_2(n!)
= log_2(n!)
For a lose upper bound:
log_2(n!) = log_2(n x n-1 x n-2 x .. x 1) = log_2(0) + log_2(1) + log_2(3) + .. + log_2(n) = n x log_2(n)
=~ n log_2(n)
= O(n log_2(n))